Tema de Investigación

Para terminar y poner fin a esta aventura matemática os dejamos el último tema. 

TABLAS Y GRÁFICAS ESTADÍSTICAS

¿Qué es una tabla estadística?

Es un cuadro que se usa para organizar, clasificar y resumir datos relevantes que se ha recolectado, con la finalidad de informarse sobre algún tema. 

Su uso permite registrar, ordenar y resumir los resultados cuantitativos recolectados de alguna variable investigada, así como establecer relaciones entre diversas variables.

Variable estadística: es cada una de las características o cualidades que poseen los individuos de una población. Puede ser: 

• Cuantitativa: las características que pueden ser medidas con números, por ejemplo: número de trabajadores en una fábrica. 
• Cualitativa: las características que no pueden ser medidas con números. Por ejemplo: qué deportes les gustan más a los alumnos.

Las variables cualitativas no se pueden representar en números, pero se pueden:

• Clasificar por el nombre.

• Ordenar según algún tipo de gradación, por ejemplo, no me gusta, me gusta, me encanta...

Las variables cuantitativas pueden expresarse en números y se conocen como: 

• Variables discretas: Son el resultado de contar y toman valores enteros.

• Variables continuas: Son el resultado de medir y se expresan en números decimales. Ejemplo 25 m2.

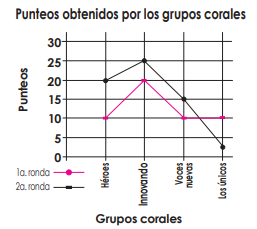
¿Qué es una gráfica estadística?

Es un dibujo utilizado para representar la información recolectada, que tienen entre otras funciones: 

• Representar los datos de forma visible. 
• Hacer visibles los posibles cambios de esos datos en el tiempo y en el espacio. 
• Establecer de forma clara la relaciones que pueden existir en los datos que representa. 
• Sintetizar los datos. 
• Complementar las tablas con otros datos o ayudas

Tipos de gráficas estadísticas:

• Gráfica de barras y columnas.

• Gráfico de columnas múltiples.

• Gráfico de líneas.

• Histogramas.

• Gráficas circulares.

MEDIA ARITMÉTICA, MODA, MEDIANA Y RANGO.

Media Aritmética

La media aritmética es la suma de todos los datos dividida entre el número total de datos.

Ejemplo:

- Datos: 6 balones de fútbol, 5 pelotas de tenis, 3 pelotas de ping-pong, 2 balones de baloncesto.

Número total de datos: 4

                                           6+5+3+2             16

                                       ----------------- =   ------- =   4

                                                 4                     4

Moda

La moda es el dato que más veces se repite, es decir, aquel que tiene mayor frecuencia absoluta

Ejemplo: La moda es los balones de fútbol ya que son 6.

Mediana

La mediana es el valor que ocupa el lugar central entre los valores del conjunto de datos, cuando estos están ordenados en forma creciente o decreciente.

Ejemplo: 

• 2<3<5<6 En este caso hay dos números centrales por lo que haremos 5+3 dividido entre dos es igual a 4. El 4 es la mediana.

• Si hubiera un número de datos impares sería: 2<3<5<6<7. El 5 es la mediana. 

Rango

Se calcula restando el valor máximo al valor mínimo.

2<3<5<6      6-2= 4 El Rango es 4.

EXCURSIÓN DÍA 10 DE ABRIL

Buenos días chicos, desde el departamento de matemáticas estamos preparando una excursión para ir a Micropolix, ya que allí pondréis en practica las mates de una forma divertida, porque tendréis dinero que tendréis que gastar, ganar e invertir y para ello tendréis que saber sumar y restar. Las matemáticas están presentes en toda nuestra vida como veis.

Hora de salida del colegio: 09:10 horas

Hora de llegada a Micropolix: 9:50 horas

Después de llegar a Micropolix, os daremos total libertad para que vayáis por vuestra cuenta, pero a las 14:20 quedaremos en el comedor para comer toda la clase junta. Después de comer, tendréis otra vez total libertad para ir donde queráis pero a las 18:00 tenéis que estar en la puerta de la entrada sin llegar a salir. Allí nos encontraremos todos para posteriormente irnos a casa.

Hora de salida de Micropolix: 18:15

Hora de llegada al colegio: 19:00

El precio de la excursión es de 20 € por niño. En este precio entra la entrada a Micropolix y el bus de ida y de vuelta. 

OS ADJUNTO EL DOCUMENTO QUE TENEIS QUE TRAER FIRMADO POR VUESTROS PADRES PARA PODER IR A LA EXCURSIÓN.

Tema 7: Actividad con un mapa

Buenas tardes chicos, ¿creéis que conocéis bien el colegio? Bueno pues mañana veremos si es así. Os mandamos un mapa del instituto que tenéis que imprimir porque mañana haremos una actividad por grupos que consistirá en que uno de los integrantes del grupo esconderá un objeto y después ira dando indicaciones en el mapa a los demás miembros del grupo para que consigan encontrarlo. Recordar que tenéis que miraros la teoría de lo que vimos el otro día sobre lo que es un mapa antes de venir a clase para poder hacer la actividad. ¡Un saludo, matemáticos!

Tema 7: Sistema de coordenadas

Bueno chicos,como vimos ayer en clase las coordenadas cartesianas y vemos que quedaron algunas dudas respecto a esto, os subo un resumen de estas. En el también hay ejemplos de la representación de puntos el plano y finalmente una serie de ejercicios que tenéis que hacer para pasado mañana. Un saludo, chicos.

El sistema de coordenadas

Las coordenadas cartesianas es el nombre que se da al sistema para localizar un punto en el espacio.
¿Cómo funcionan las coordenadas cartesianas?
-Nos moveremos primero en horizontal: de izquierda a derecha y esa será nuestra coordenada x. 
Eje x: eje de abcisas
-Después, nos moveremos en vertical de arriba a abajo y esa será nuestra coordenada y. 
Eje y: eje de ordenadas
Los ejes de coordenadas cartesianas: 
a) Se numeran como la recta entera
b) Son perpendiculares y se cortan en el cero.
c) Dividen la cuadricula en cuatro partes que se llaman cuadrantes.

¿Cómo representamos un punto en el plano?
Un punto se representa en el plano con dos coordenadas. 
La primera se lee con el eje x o de abcisas.
La segunda se lee con el eje y o de ordenadas.
Ejemplos de puntos: (3,1)
                                 (-2,4)
                                 (-4,-2)
                                 (2,-3)

Representa los siguientes puntos en el plano:
a) (5,-9)                                                                           e) (-7,5)
b) (-7,-8)                                                                          f) (-1, 4)
c) (4, 6)                                                                            g) (-3,-2)
d) (8,8)                                                                             h) (6, -2)

NOTICIA. Matemáticas avanzadas... ¿sirven para algo?

Hola chicos, muchas veces os habéis preguntado si las matemáticas en un nivel avanzado son realmente válidas o no, ya que nunca vamos a usar derivadas para comprar el pan, o jamás vamos a usar Ruffini para resolver un problema de nuestra vida diaria, pero ¿y si hablamos de problemas que podrían acabar con el planeta?

Pues bien, un grupo de investigadores de la Universidad Autónoma de Barcelona (UAB)  del Centre de Recerca Matemàtica (CRM) y de la Barcelona Graduate School of Mathematics (BGSMath) han sido capaces de encontrar fórmulas generales para prevenir eventos catastróficos. A estas fórmulas se les llama bifurcaciones y permites describir cambios cualitativos en la dinámica de un sistema cuando un parámetro de control cambia.

Estas bifurcaciones se encuentran en fenómenos físicos, reacciones químicas, láseres, experimentos de laboratorio con células, modelos climáticos... pero en matemáticas explican la dinámica del sistema considerando su evolución en un tiempo infinito. La importancia de los investigadores que hemos nombrado anteriormente es que han encontrado las fórmulas para un tiempo finito determinado.

Gracias a este método, la extinción de especies o el cambio climático, podremos observar si un sistema acercándose a un cambio tendrá un bifurcación suave o catastrófica. Esto último quiere decir que llegará a un punto de no retorno, el daño será irreversible.

Estas leyes nos ayudarán a prevenir y dar "señales de alerta", han descubierto eventos irreversibles como, por ejemplo, extinciones, reacciones químicas extremas o el deshielo en los polos.

https://noticiasdelaciencia.com/art/30213/formulas-matematicas-para-anticipar-eventos-catastroficos 

Tema 7: Error proporcionalidad

Buenas chicos, como ya sabéis, el otro día vimos en clase la resolución de proporcionalidad directa a través de diferentes formas.

En este caso, será a través del proceso de "Reducción a la unidad".

Primero, os pondremos el enunciado del problema, más tarde la resolución y por último, una serie de soluciones en la cuales tendréis que identificar cuál es la correcta.

¡Suerte!

En una obra 8 ingenieros acaban en 10 días de excavar un hoyo de 50 metros de profundidad. ¿Cuántos ingenieros son necesarios para conseguir un hoyo de 200 metros de profundidad en 15 días?

Realiza el siguiente procedimiento:

Las soluciones a este problema son:

a) El alumno ha razonado adecuadamente el problema y la solución es correcta.

b) El alumno ha razonado bien el problema pero la solución es incorrecta debido a un error en el procedimiento.

c) El alumno ha razonado mal el problema y por eso, la solución es incorrecta.

d) El alumno ha razonado mal el problema pero la solución es correcta.

¡Mucha suerte!

Tema 7: Problema TIMSS

Os dejamos por aquí un problema de tipo TIMSS como el que vimos en la clase anterior, y aprovechando que es la semana de los deportes en el colegio, os lo relaciono de la siguiente manera:

1 pelota de tenis= 3 pelotas de ping pong.

2 pelotas de tenis= 5 pelotas de fútbol.

Dado estos datos, si Julia tenía 5 pelotas de fútbol para cambiarlas por pelotas de ping pong. ¿Cuántas puede conseguir?

Mucha suerte, y.. ¡¡a ver quien es capaz!!

Tema 5 y 6: Ejercicios Proporcionalidad directa.

Os dejamos una serie de ejercicios que deberéis traer resueltos para el próximo día de clase, aunque no os salga alguno debéis intentarlo, los corregiremos en clase y resolveremos las dudas que os surjan.

Ejercicios:

1) Trescientos gramos de queso cuestan 6€ ¿Cuánto podré comprar con 4,50€?

2) Un camión a 60 km/h tarda 40 minutos en cubrir cierto recorrido. ¿Cuánto tardará un coche a 120 km/h?

3) Por tres horas de trabajo, Alberto ha cobrado 60 € ¿Cuánto cobrará por 8 horas?

4) Por 5 días de trabajo he ganado 390 euros. ¿Cuánto ganaré por 18 días?

5) Una máquina embotelladora llena 240 botellas en 20 minutos. ¿Cuántas botellas llenará en hora y media?

6) Un coche que va a 100 km/h necesita 20 minutos en recorrer la distancia entre dos pueblos. ¿Qué velocidad ha de llevar para hacer el recorrido en 16 minutos?

7) Un corredor de maratón ha avanzado 2,4 km en los 8 primeros minutos de su recorrido. Si mantiene la velocidad, ¿cuánto tardará en completar los 42 km del recorrido?

8) Un camión que carga 3 toneladas necesita 15 viajes para transportar cierta cantidad de arena. ¿Cuántos viajes necesitará para hacer transportar la misma arena un camión que carga 5 toneladas?

9) Un ganadero tiene 20 vacas y pienso para alimentarlas durante 30 días. ¿Cuánto tiempo le durará el pienso si se mueren 5 vacas?

10) En un campamento de 25 niños hay provisiones para 30 días. ¿Para cuántos días habrá comida si se incorporan 5 niños a la acampada?

11) Un taller de ebanistería, si trabaja 8 horas diarias, puede servir un pedido en 6 días. ¿Cuántas horas diarias deberá trabajar para servir el pedido en 3 días?

12) Tres obreros descargan un camión en dos horas. ¿Cuánto tardarán dos obreros?

Tema 5 y 6

Hola chic@s hoy vamos a repasar lo explicado en clase, la regla de tres con proporcionalidad directa, a continuación os dejamos unos apuntes para que vuestro estudio sea más fácil y podáis realizar los problemas cómodamente.

Regla de tres: Proporcionalidad directa.

La regla de 3 simple es una operación que nos ayuda a resolver rápidamente problemas de proporcionalidad, tanto directa como inversa.

Para hacer una regla de 3 simple necesitamos 3 datos: dos magnitudes proporcionales entre sí, y una tercera magnitud. A partir de estos, averiguaremos el cuarto término de la proporcionalidad.

Colocaremos en una tabla los 3 datos (a los que llamamos “a”, “b” y “c”) y la incógnita, es decir, el dato que queremos averiguar (que llamaremos “x”). Después, aplicaremos la siguiente fórmula:

                                     

                                     

Ejemplo:

Al llegar al hotel nos han dado un mapa con los lugares de interés de la ciudad, y nos han dicho que 5 centímetros del mapa representan 600 metros de la realidad. Hoy queremos ir a un parque que se encuentra a 8 centímetros del hotel en el mapa. ¿A qué distancia del hotel se encuentra este parque?

Vamos a hacer la tabla con los 3 datos y la incógnita (“x”), y hallaremos “x” con la fórmula que acabamos de aprender:

                        

                                     

Solución: El parque se encuentra a 960 metros del hotel

*Es importante que tengáis especial atención a la hora de colocar los datos en la tabla.

TEMA 5 Y 6

Proporcionalidad geométrica

Teorema de Tales

¡Hola chicos, muy buenos días! En el día de hoy os vamos a recordar que es el Teorema de Tales y como podemos aplicarlo a problemas. 

EL teorema de Tales se considera el teorema fundamental de la semejanza de triángulos y establece lo siguiente:

• Toda recta paralela a un lado de un triángulo, forma con los otros dos lados o con sus prolongaciones otro triángulo que es semejante al triángulo dado.

 Lo primero que haremos es ver que nos dice este teorema:

1. Si dos rectas cualesquiera se cortan por varias rectas paralelas, los segmentos determinados en una de las rectas son proporcionales a los segmentos correspondientes en la otra. 
2. Dado un triángulo ABC, si se traza un segmento paralelo, B'C', a uno de los lados del triangulo, se obtiene otro triángulo AB'C', cuyos lados son proporcionales a los del triángulo ABC.

Ejemplos:

LOCALIZAR LUGARES

Para localizar lugares debemos conocer todas las direcciones, para saber a donde vamos, buscar objetos en casa, etc...

CROQUIS

Es un dibujo rápido hecho a mano alzada, sin escalas ni medidas.

BRÚJULA

La brújula es un instrumento para orientarnos en cuanto a los puntos cardinales.

Un truco para saber manejar los puntos cardinales, es usar nuestro cuerpo de referencia. Si extendemos nuestros brazos y hacemos que el brazo derecho señale la salida del sol y el izquierdo por donde se oculta, sabemos que delante está el norte, detrás el sur, a la izquierda el oeste y a la derecha el este.

CARTOGRAFÍA

Es la ciencia y el arte que enseña a representar total total o parcialmente el globo terrestre en una su Los planos y los mapas son dos tipos de representaciones lineales que difieren entre sí en función de su contenido y la forma como está realizado.

PLANO

Es una representación gráfica en dos dimensiones (2D) y tamaño reducido (a escala) de un terreno o territorio real (3D). Es decir, es un dibujo que trata de representar un espacio real o un paisaje, pero visto desde arriba, como si lo observásemos desde un avión. Hay distintos tipos:

• Planos topográficos: representan el relieve de una determinada superficie.

• Planos arquitectónicos: representan detalles de construcciones u obras arquitectónicas.

• Planos estructurales: representan estructuras de columnas, cimentación, vigas, entre otros. 

• Planos de instalaciones: representan las instalaciones sanitarias, hidráulicas, eléctricas, entre otras.

• Planos urbanísticos: representan zonas urbanas con sus calles, avenidas áreas residenciales, de recreación, entre otras.

• Planos de maquinarias: donde se representan detalles de las maquinarias y equipos.

MAPAS

Los mapas son representaciones planas de una parte o de la totalidad de la superficie terrestre. Es una representación, es decir no es la realidad exacta. Es como una foto tuya donde no eres tú sino una representación plana de ti mismo

Las principales diferencias entre ellos son: 

• Los mapas figuran espacios mayores que los espacios de un plano, como son el de una ciudad, un país o el mundo, por lo tanto, no tienen tantos detalles como los planos.
• Los mapas utilizan proyección cartográfica para tomar en cuenta la curvatura de la tierra y se ubican a través de una red que consta de los meridianos y paralelos mientras que los planos no utilizan proyección cartográfica para representar elementos. 
• Los mapas se utilizan más que todo para ubicarse en un lugar, desde una compañía, nave industrial, ciudad u otros mientras que los planos se utilizan mayormente para dar detalles acerca de una maquinaria, un elemento, una construcción, instalaciones, entre otros.

ESCALA

El termino escala es la sucesión ordenada de un conjunto de términos de una misma calidad. La escala de una unidad refiere a la medida que se debe tomar en cuenta a la hora de reducir o ampliar algo para que su representación física o dibujada sea más fácil de interpretar. Ejemplo: Un edificio muy grande necesita un modelo a escala mas pequeña para que los ingenieros y arquitectos puedan visualizar mejor su geometría. 

TEMA 5 Y 6 EJRCICIOS

EJERCICIOS
1) Usa el Teorema de Tales para resolver x:

2) Calcula el valor de x aplicando el Teorema de Tales:

3) Halla x e y aplicando el Teorema de Tales

4) Halla x aplicando el teorema de Tales

5) Las baldas de una repisa representada en la figura son paralelos. Calcula las longitudes de la repisa representadas como x e y.

Tema 4: Tangram

El otro día vimos en clase los demás tangrams.

¡Hoy veremos el tangram de 5 piezas!

Realizaremos algunas de las figuras geométricas que hemos visto en clase.

¿Estáis listos? 

¡Vamos a por ello!

Triángulo

Rectángulo

Rombo

Romboide

Esto es todo por hoy chicos, espero que hayáis sido capaces de hacer todas las figuras. Para finalizar os proponemos un reto... a ver quien es capaz de hacer cualquier figura con un tangram de 6 piezas. ¡Hasta la próxima!

Tema 4: Tangram

Como ya vimos en clase, el tangram es un juego chino muy antiguo, que consiste en formar siluetas de figuras con las siete piezas dadas sin solaparlas. Las 7 piezas, llamadas "Tans", son las siguientes:

-5 triángulos, dos construidos con la diagonal principal del mismo tamaño, los dos pequeños de la franja central también son del mismo tamaño.
-1 cuadrado
-1 paralelogramo o romboide

Normalmente los "Tans" se guardan formando un cuadrado.

No solo existe tangram de 7 piezas sino que existen de 3, 4, 5 y 6 piezas. Hoy vamos a practicar distintas figuras con los tangram de 3 y 4 piezas. ¿Estáis listos? Pues vamos a por ellos.

Tangram de 3 piezas

Triángulo rectángulo

Triángulo isósceles

Rectángulo

Romboide

Trapecio isósceles

Tangram de 4 piezas

Triángulo isósceles

Trapecio isósceles

Romboide

Rectángulo

Esto es todo por hoy chicos, el próximo día haremos las figuras del tangram de 5 y 6 piezas. Espero que hayáis conseguido hacer todos, y si no es así el próximo día en clase os ayudaremos a hacerlos ¡Un saludo!